CoderEthan学习站

深色模式

004_Activation

学习任何模块的知识一定要从全局视角俯视，至少要知道处于哪个位置，知道在解决哪方面的问题

1. 为什么需要激活？ ​

深度学习往往只说非线性Attention，当然也有线性激活

相关的论文我就不添加了，可以随便找到的

在深度学习模型中，为啥在每一层输出后基本都要加入一层激活层？主要原因是让模型具有非线性能力（你可能需要花两分钟补充一下线性和非线性的相关概念），当然还有其他的作用，我们暂且不考虑那么多（好吧，让我自己说也说不出来多少），不妨慢慢研究，整理过程中不断发现其中的奥妙所在。

其实在最初的时候，激活的想法跟我们的神经元激活现象有点类似，可能就是这种想法慢慢引入的（笔者瞎说的）

思考：

  • 为啥不用线性激活？又或者说不使用非线性激活会出现怎样的情况？
  • 激活是对数据的怎样的一个操作？是point-wise（或者element-wise）类型操作还是？（可能需要花两分钟补充一下这些代名词）
  • 让你设计你会设计出一个怎样的激活函数？
  • 可否设计一种激活，是将输入进行非线性操作的基础上进行升维或者降维操作？（这是笔者在思考的，当然在学习过程中可能会进行尝试）

2. 类型 ​

激活函数其实可以按不同的划分方式进行分类，但我不再进行分类，只是罗列出一些常用的激活。

注意：所有图像的横坐标轴数据可能与显示数值无关哈

2.0 简单总结（AI辅助的） ​

激活函数数学表达式优点缺点适用场景
Sigmoid11+e−x\frac{1}{1 + e^{-x}}输出在 (0,1)，适合概率输出梯度消失、非零均值、计算较慢二分类输出层
Softmaxexi∑jexj\frac{e^{x_i}}{\sum_j e^{x_j}}多分类概率分布，输出总和为 1对极端值敏感，计算成本高多分类输出层
Tanhex−e−xex+e−x\frac{e^x - e^{-x}}{e^x + e^{-x}}输出在 (-1,1)，零均值梯度消失问题RNN、数据对称场景
ReLUmax(0,x)\max(0, x)计算高效，缓解梯度消失神经元死亡（负值输出为 0）CNN、默认隐藏层激活
Leaky ReLU{xif x≥0αxif x<0\begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 \end{cases}缓解神经元死亡问题需手动调参（如 α=0.01）深层网络替代 ReLU
PReLULeaky ReLU，但α可学习自适应斜率，更灵活增加参数量复杂任务、深层网络
ELU{xif x≥0α(ex−1)if x<0\begin{cases} x & \text{if } x \geq 0 \\ \alpha(e^x - 1) & \text{if } x < 0 \end{cases}平滑负值，缓解梯度消失计算复杂（含指数运算）需要处理负值的场景
GELUx⋅Φ(x)x \cdot \Phi(x) Φ 为标准正态 CDF平滑柔和，适合深度网络计算复杂Transformer、BERT 等模型
Swishx⋅σ(βx)x \cdot \sigma(\beta x)（β可调）非单调，实验性能优于 ReLU计算较复杂EfficientNet 等先进网络
Mishx⋅tanh(ln(1+ex))x \cdot \tanh(\ln(1 + e^x))平滑、无上界，缓解梯度消失计算成本高计算机视觉任务

2.1 Sigmoid ​

Sigmoid（又称Logistic），在数学或者计算机领域的推导特别漂亮，单这里我不再进行推导。（可以使用概率相关知识和极大似然估计等推导）

Sigmoid(x)=σ(x)=11+exp(−x)\text{Sigmoid}(x) = \sigma(x) = \frac{1}{1 + \exp(-x)}

Sigmoid(x)′=Sigmoid(x)∗(1−Sigmoid(x))\text{Sigmoid}(x)' = \text{Sigmoid}(x) * (1 - \text{Sigmoid}(x))

  • 他是一种point-wise类型的非线性激活

  • 将输入映射到（1, 0），且单调性不变

  • 函数与导函数图像（是一种S型激活）

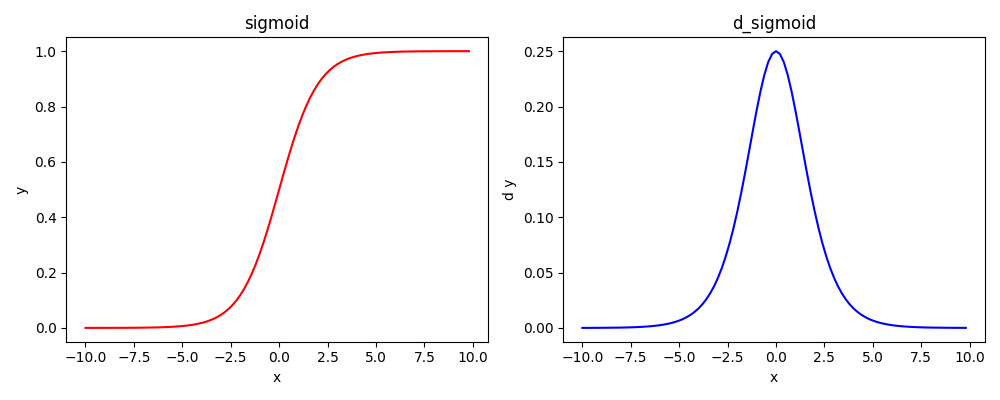
    image-20250408113044493

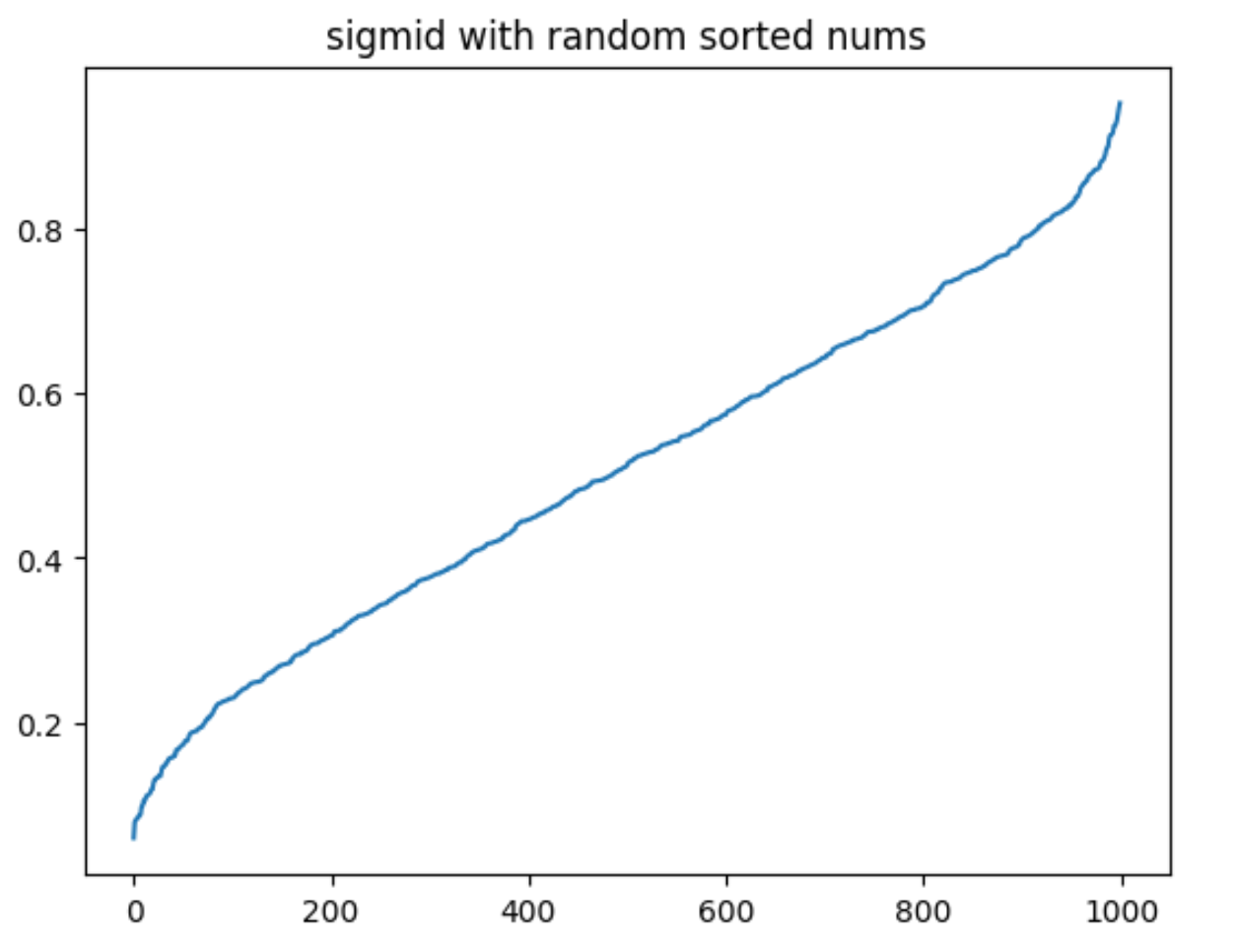
  • 随机数据（排序后）测试图像

    有没有觉得跟DyT的实现效果有点像

    image-20250505160309198

思考：

  • 在NLP任务中，激活操作的维度是尊三哪个维度？还是不指定维度也可以？

2.2 Tanh ​

Tanh(x)=tanh(x)=exp(x)−exp(−x)exp(x)+exp(−x)\text{Tanh}(x) = \tanh(x) = \frac{\exp(x) - \exp(-x)} {\exp(x) + \exp(-x)}

Tanh(x)′=1−(Tanh(x))2\text{Tanh}(x)' = 1 - (\text{Tanh}(x))^2

  • 同样是一种point-wise类型的非线性激活

  • 将输入映射到（-1, 1），且单调性不变

  • 函数与导函数图像（是一种S型激活）

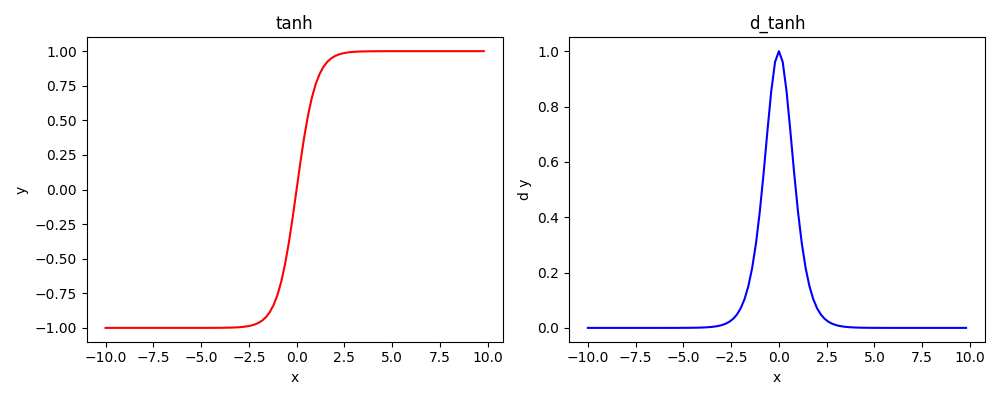
    image-20250408114522622

  • Sigmoid和Tanh的对比

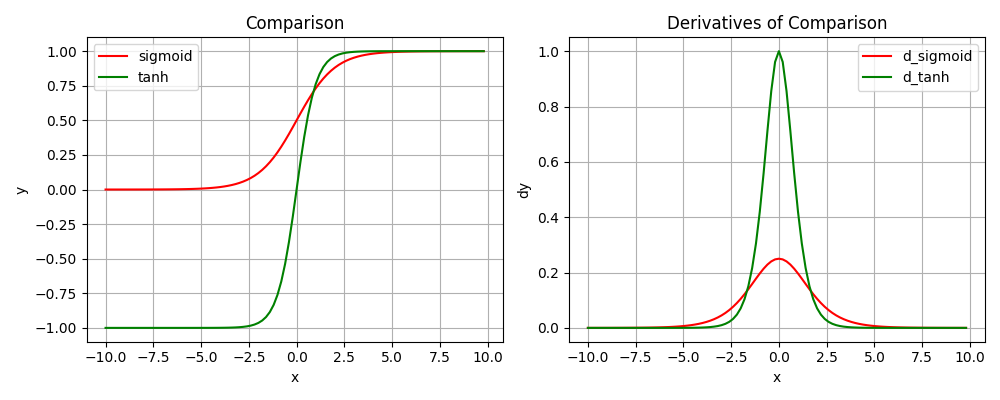
    image-20250408150852517

2.3. ReLU ​

当时的AlexNet论文（我记得是）里面使用，结果吊打其他激活

现在很多常用的激活都是在该激活上进行优化的

ReLU=max(0,x)ReLU = max(0, x)

  • 同样是一种point-wise类型的非线性激活

  • 将输入映射到（0, +∞），且单调性不变

  • 函数与导函数图像（是一种S型激活）

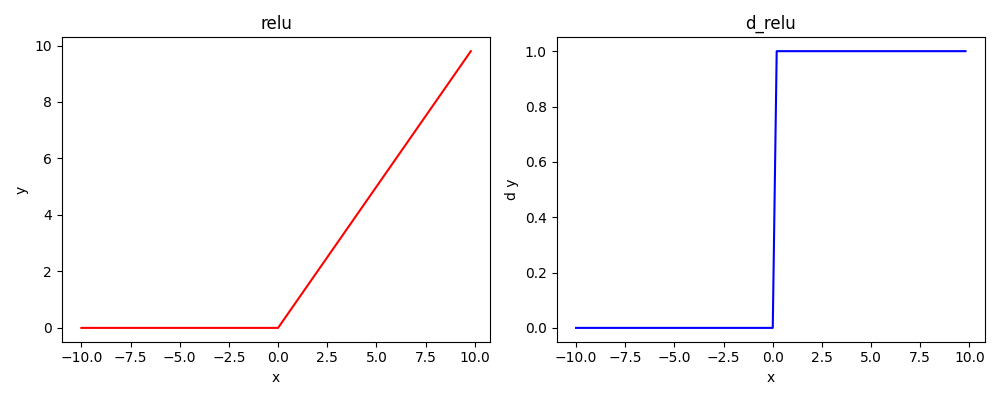
    image-20250408115631449

2.4 其他ReLU变种 ​

不同Markdown渲染工具可能对LaTex公式渲染效果不同，可能产生乱码现象，所以这里用一张图片展示公式

原公式需要的可以用图片公式识别工具，或者后台找我索要

image-20250505163711905

  • 当然ReLU相关的激活还有，下面也会讲到一些更常用的

2.5 GeLU ​

工程实际上是进行了简化的

其实后面的激活有些感觉像凑图像了

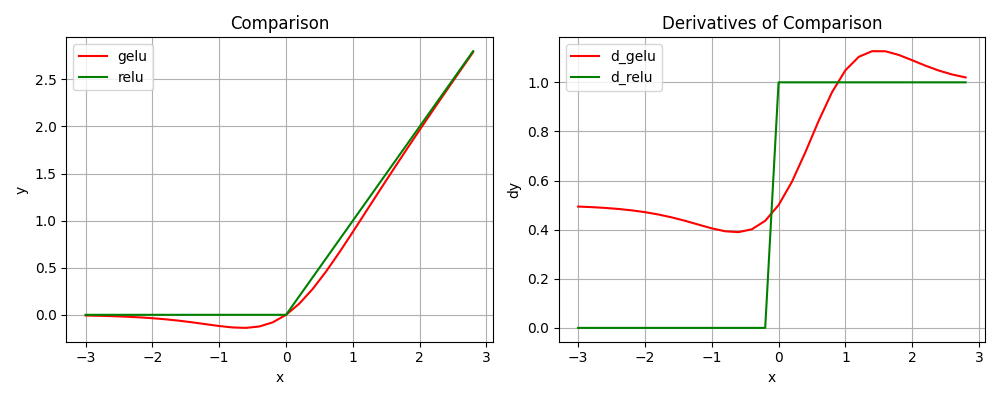
GELU(x)=xP(X≤x)=xΦ(x) xΦ(x)≈xσ(1.702x) xΦ(x)≈\frac{1}{2} ×[1+tanh(\sqrt{\frac{π}{2}}(x+0.044715x^3))]

  • 大模型常用的激活

  • 图像对比

    image-20250408175719134

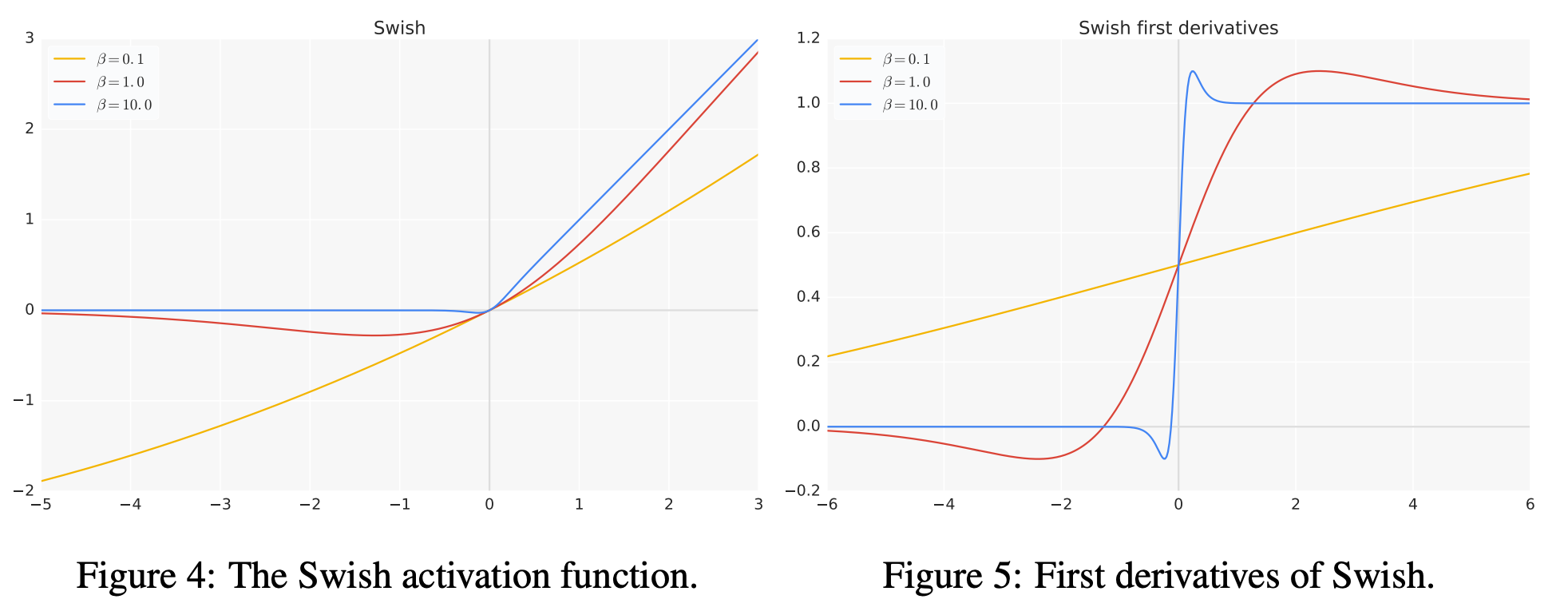
2.6 swish类型 ​

图像我就使用论文里面的图像了

  • Swish
Swish = x·Sigmoid(\beta x)

(Swish)′=βSwish+Sigmoid(βx)∗(1−Sigmoid(βx))(Swish)' = \beta Swish + Sigmoid(\beta x) * (1 - Sigmoid(\beta x))

image-20250505165029524
  • Hard Swish
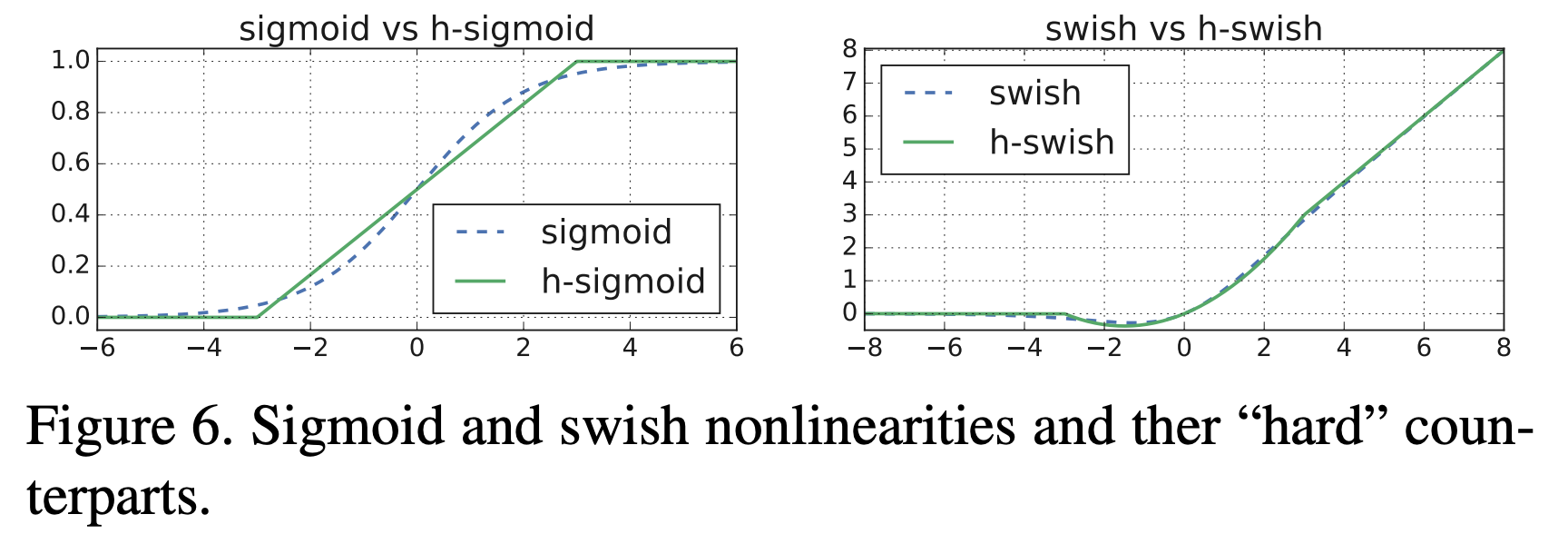
Hard\ Swish = x·\frac{ReLU6(x + 3)}{6}

image-20250505165925039

2.7 Mish ​

Mish(x)=x∗Tanh(Softplus(x))\text{Mish}(x) = x * \text{Tanh}(\text{Softplus}(x))

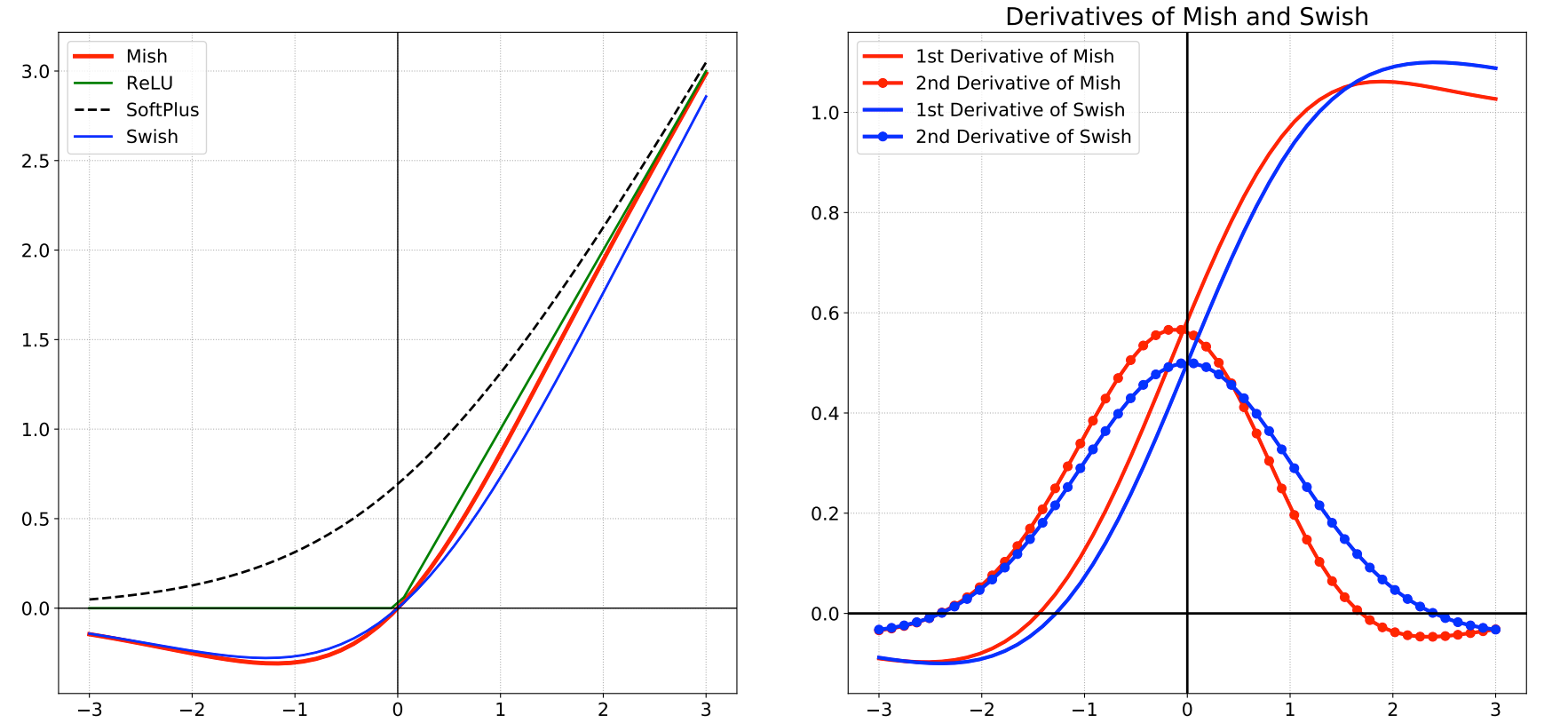
image-20250505172202489

2.8 Softmax ​

这个在深度学习中通常在最后一层的概率归一使用，其实他是从sigmoid过来的

Softmax(xi)=exi∑jexj\text{Softmax}(x_{i}) = \frac{e^{x_i}}{\sum_je^{x_j}}

∂yi∂xj={yi(1−yi),if i=j−yiyj,if i≠j\frac{\partial y_i}{\partial x_j} = \begin{cases} y_i (1 - y_i), & \text{if } i = j \\ - y_i y_j, & \text{if } i \ne j \end{cases}

J=[y1(1−y1)−y1y2⋯−y1yn−y2y1y2(1−y2)⋯−y2yn⋮⋮⋱⋮−yny1−yny2⋯yn(1−yn)]J = \begin{bmatrix} y_1(1 - y_1) & -y_1 y_2 & \cdots & -y_1 y_n \\ -y_2 y_1 & y_2(1 - y_2) & \cdots & -y_2 y_n \\ \vdots & \vdots & \ddots & \vdots \\ -y_n y_1 & -y_n y_2 & \cdots & y_n(1 - y_n) \end{bmatrix}

  • 这种就不是point-wise类型了，你把公式拆开看就知道其实每个输出都与其它输入相关

  • 💡 实际意义

    Softmax 的原函数/导数都不是与输入独立的，每个输出值/梯度都跟其它的有关。

  • Torch源码里面有所优化

Softmax(xi)=exi−max(x)∑jexj−max(x)\text{Softmax}(x_{i}) = \frac{e^{x_i - max(x)}}{\sum_je^{x_j - max(x)}}

3. 代码实现 ​

都是公式，直接抄公式就行啦

4. 面试考点 ​

5. 思考 ​

  • 对于类似softmax这种同一条数据的分母相同的，每次是否需要重新计算分母？（底层是否会做cache？）
  • PyTorch源码里面的Softmax激活提及了NLLLoss，这是什么？与交叉熵又是什么关系？
  • softmax的导数推导（好像这种求导中间矩阵被称为雅克比矩阵）。
  • softmax输入的shape和梯度的shape不一样大吗？参数更新的时候又是怎样子的？