002_Normalization

1. 引入

1.1 为啥Norm？

由于在模型训练的时候往往层数较多，我个人尝试过，如果对输入和中间层不进行归一化操作，往往收敛效果比较差。但是我又在思考，在每模型结构的每层输出之后不都有一个非线性操作吗，很多都有类似缩放的操作，为什么还要进行Norm？于是我查阅了相关的原始论文，原来是因为：每层的激活输出会影响数据的分布情况，而进行Norm后的数据分布，在梯度计算的时候更容易进行收敛（这是结论，具体原因相关论文有指出，下面思考也进行了标注）。还有一点就能能够起到一定的正则化效果。

当然，我暂时对数据分布情况的了解和测试几乎为0，所以只能感受到一个大致的思想，后续再慢慢细磨也不迟，大方向没问题对我来说很重要。

这里引用一下RMS Norm作者的原话：

"One bottleneck deep neural networks have been hypothesized to suffer from is the internal covariate shift issue [27], where a layer’s input distribution changes as previous layers are updated, which significantly slows the training.1"
“深度神经网络被假设存在的一个瓶颈是 内部协变量偏移 问题 [27]，其中层的输入分布随着先前层的更新而变化，这会显著减慢训练速度。1”

1.2 作用

解决多层神经网络中间层的协方差偏移（Internal Covariate Shift）
缓解梯度消失/爆炸（Gradient Vanishing/Explosion）
在LN论文里面好像有说明（也可能是在BN论文里面）
加速模型收敛
对权重初始化的依赖降低（AI说的）
想想权重初始化的方式有哪些？（论文支撑）

思考：

在NLP任务中，是在哪个维度进行Normalize？

都进行过Softmax操作了，为啥还需要进行Normalize？

2. 类型

类型	公式	特点/应用场景
Batch Norm	$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$	等长序列（cv）
Layer Norm	$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$	变长序列（nlp）
RMS Norm	$y_i = \frac{x_i}{\mathrm{RMS}(x)} * \gamma_i, \quad \text{where} \quad \text{RMS}(x) = \sqrt{\epsilon + \frac{1}{n} \sum_{i=1}^{n} x_i^2}$	LN的一种优化
DyT	$\gamma * Tanh(\alpha * x) + \beta$	暂定（2025最新论文）
……	……	……

2.1 Batch Norm

中英文对比论文：Batch Norm

$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$

关键四步
训练和推理
NOTE
但是这里有一个点注意一下，在训练的时候有Batch的训练，但是推理的时候可以是任意的（比如单一的数据输入），这时候其实是没有Batch的mean（均值）和var（方差）这个概念的，所以，训练和推理的中Norm的计算方式是不一样的（PyTorch框架中的running属性进行控制），其实主要是两点（笔者个人理解）：
1. 训练中的mean和var用于推理中（想想该如何设计呢）
2. 训练的mean计算采用移动指数平均的方式（代码里面有个momentum参数，这里的跟优化器里的动量不一样哈）
  running_{mean}=(1−momentum)⋅running_{mean}+momentum⋅mean
  var同理

pytorch相关关键代码

python

if self.momentum is None:
    exponential_average_factor = 0.0
else:
    exponential_average_factor = self.momentum

if self.training and self.track_running_stats:
    # TODO: if statement only here to tell the jit to skip emitting this when it is None
    if self.num_batches_tracked is not None:  # type: ignore[has-type]
        self.num_batches_tracked.add_(1)  # type: ignore[has-type]
        if self.momentum is None:  # use cumulative moving average
            exponential_average_factor = 1.0 / float(self.num_batches_tracked)
        else:  # use exponential moving average
            exponential_average_factor = self.momentum

r"""
    Decide whether the mini-batch stats should be used for normalization rather than the buffers.
    Mini-batch stats are used in training mode, and in eval mode when buffers are None.
"""
if self.training:
    bn_training = True
else:
    bn_training = (self.running_mean is None) and (self.running_var is None)

2.2 Layer Norm

中英文对照论文：Layer Norm

$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$

数据不变性：
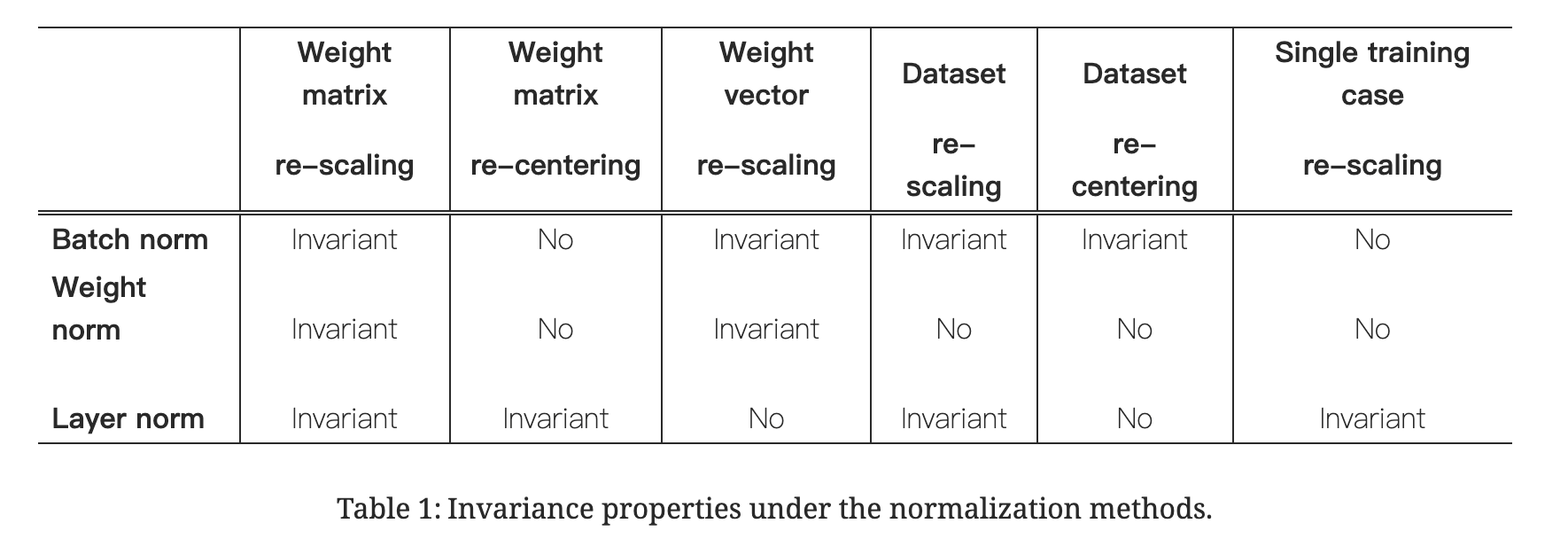
这里引用一下PyTorch官网的[!Note]:
NOTE
Unlike Batch Normalization and Instance Normalization, which applies scalar scale and bias for each entire channel/plane with the affine option, Layer Normalization applies per-element scale and bias with elementwise_affine.

这里的affine就是最后那一步放射变化，简单说就是进行缩放和平移（偏执）那一步

DeepSeek帮我稍微整理的：

归一化类型	`affine` 的作用范围	参数形状（`γ` 和 `β`）	适用场景
BatchNorm	整个通道/平面（per-channel）	`(C,)`	固定长度的批次数据
InstanceNorm	整个通道/平面（per-channel）	`(C,)`	图像生成/风格迁移
LayerNorm	每个元素（per-element）	输入张量的最后一维	变长序列（如NLP/RNN）

2.3 RMS Norm

中英文对照论文：RMS Norm

$y_i = \frac{x_i}{\mathrm{RMS}(x)} * \gamma_i, \quad \text{where} \quad \text{RMS}(x) = \sqrt{\epsilon + \frac{1}{n} \sum_{i=1}^{n} x_i^2}$

这种归一化是大模型常用的归一化层方式，原因很简单，高效！！！
核心思想（笔者理解）：去掉Layer Norm中的平移操作（平移不会影响相对分布），分母采用均方根代替。
原始论文作者是假设了重新计算的居中不变性（re-centering invariance）是可有可无的：

数据不变性：

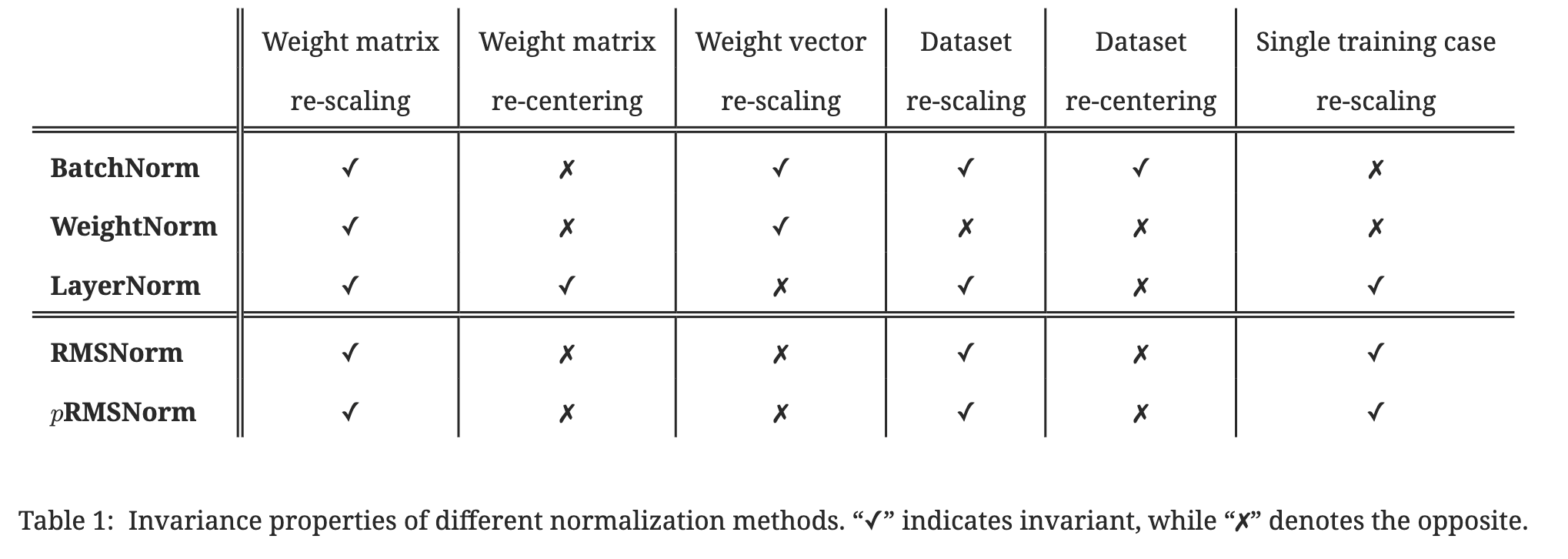
思考：

为啥偏偏就选中MSE作为规范化标准？

2.4 DyT

中英文对照论文：Transformers without normlization

$\gamma * Tanh(\alpha * x) + \beta$

灵感来源

就很随意
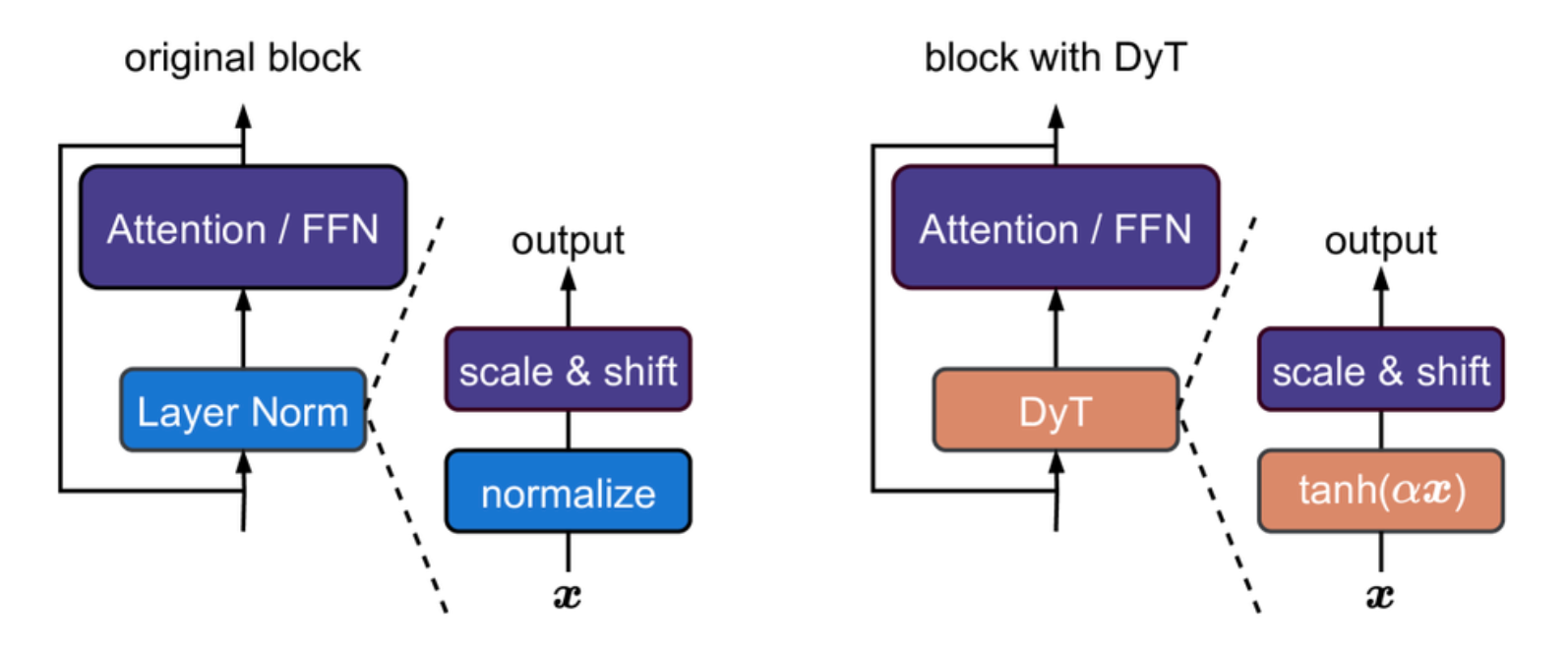
实验尝试（不同模型不同层数的Norm层前后分布对比）：
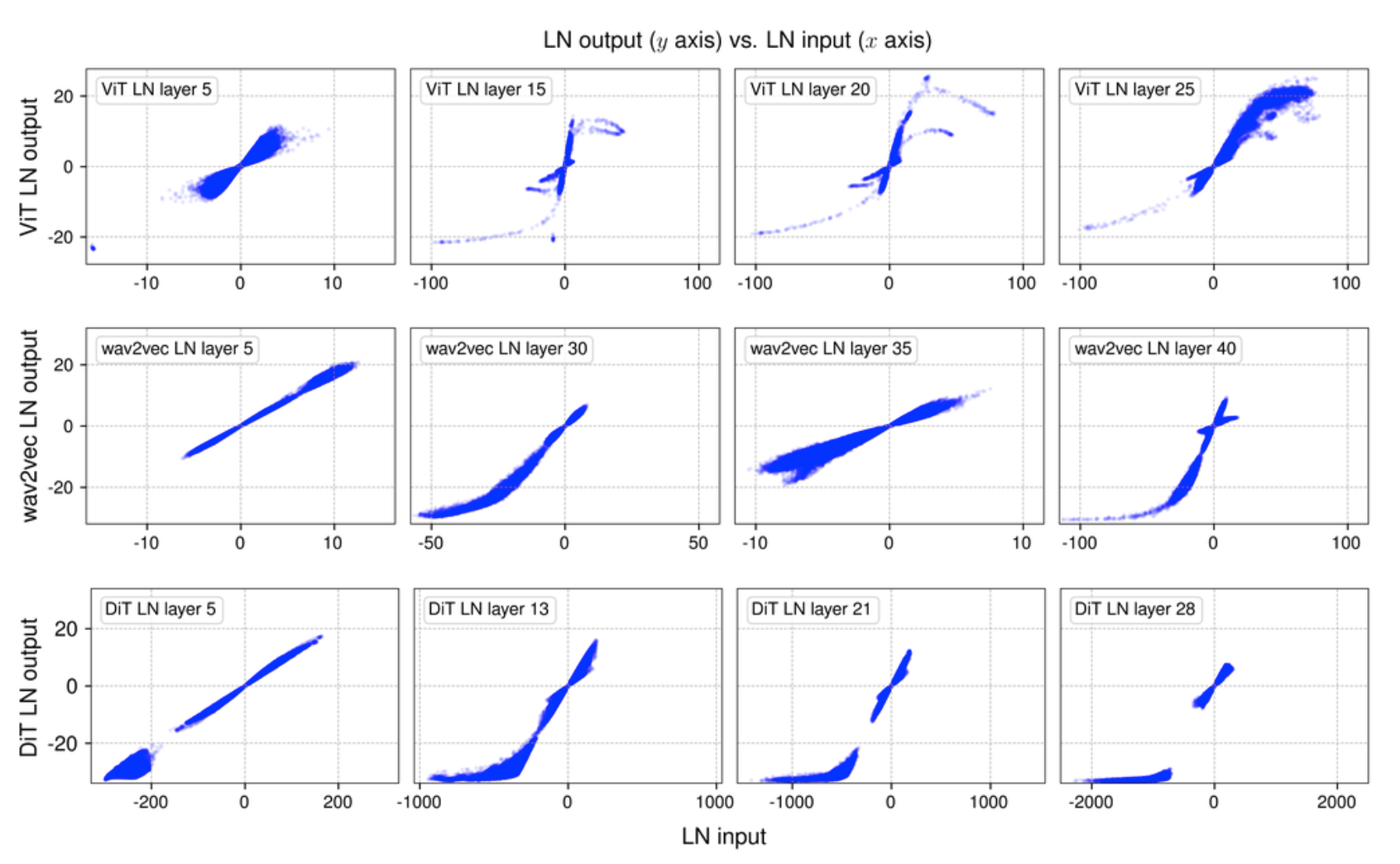
浅层的时候往往输入输出分布偏向线性
论文所给伪代码
具体尝试我暂时还未进行，就先不试了

3. 其他相关内容

3.1 Post-Norm & Pre-Norm

Pre-Norm大模型中常用
这部分内容是大模型帮我整理的（哈哈哈哈，原谅我不太想整理这块）

结构

结合Transformer那块知识，一个是在残差前，一个在残差后

Output_{post}=LayerNorm(x+SubLayer(x)) \\ Output_{pre}=x+SubLayer(LayerNorm(x)) 公式1:PostNorm(x)=x+LayerNorm(FeedForward(x+LayerNorm(Attention(x)))) \\\\ 公式2:PreNorm(x)=x+FeedForward(LayerNorm(x))+Attention(LayerNorm(x))

特性	Post-Norm	Pre-Norm
公式	公式1	公式2
位置	残差后	残差前
出现时间	原始 Transformer（Vaswani et al., 2017）	之后发展（如 GPT-2 等）
优点	收敛后表现略好（某些任务）	更稳定，训练深层模型不易梯度消失
缺点	深层模型中容易梯度消失/爆炸	可能最终性能略低，但更容易训练
应用情况	BERT、初版Transformer	GPT系列、T5、LLama等大模型

模型	归一化类型
DeepSeek	Pre-Norm
GPT-2/3/4	Pre-Norm
BERT	Post-Norm
T5	Pre-Norm
LLaMA	Pre-Norm
Transformer XL	Pre-Norm
原始 Transformer	Post-Norm

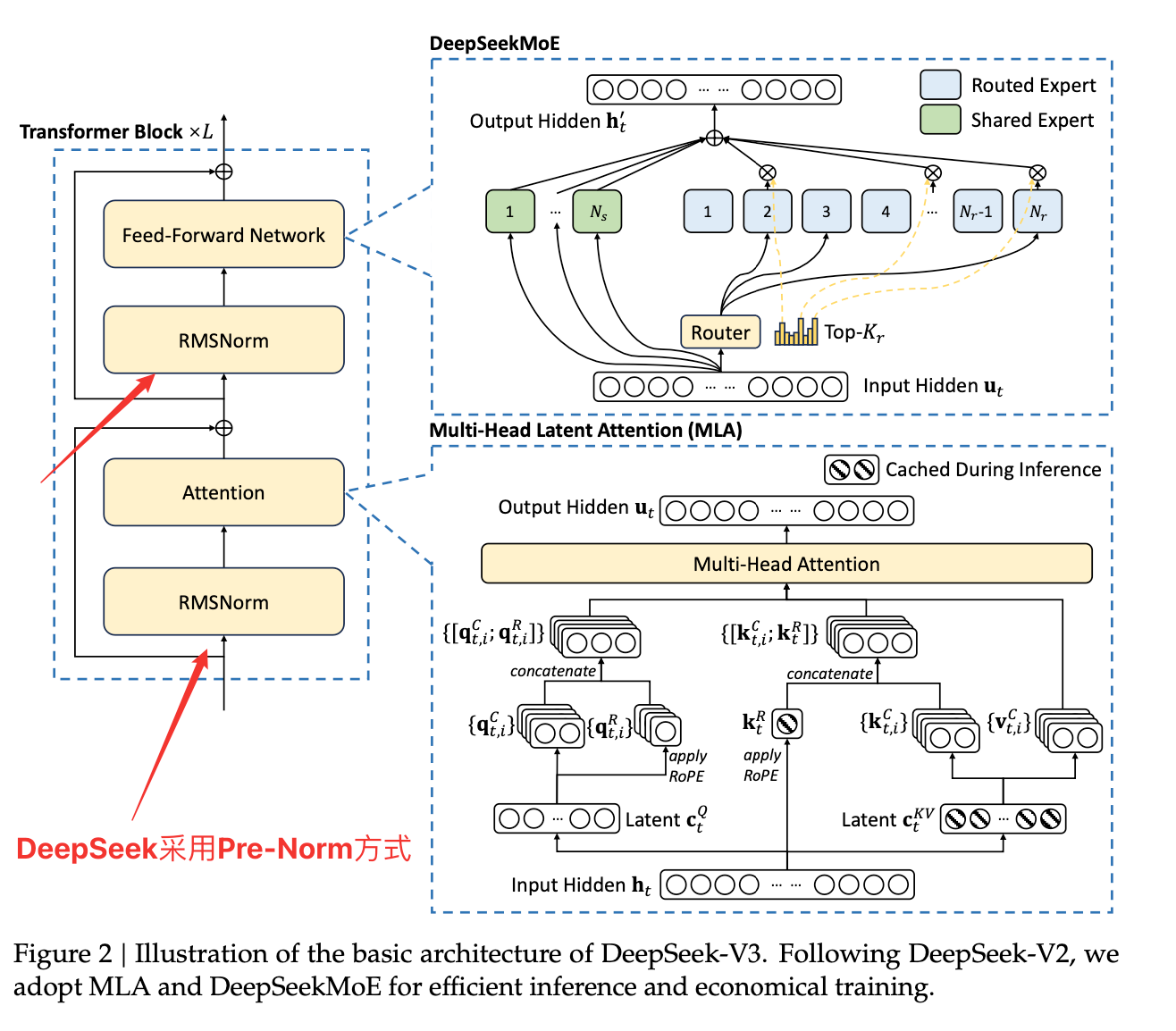
选择任务复杂度: 简单任务用 PostNorm，复杂任务用 PreNorm。模型深度: 深层模型优先选择 PreNorm。

3.2 Deep Norm

关键成果
DeepNorm 是微软在 2022 年提出的改进方法（论文 "DeepNet: Scaling Transformers to 1,000 Layers"），基于 Post-Norm 但大幅提升了深层训练的稳定性，可支持超深层（如 1000 层）Transformer 的训练。
基本结构

原始残差结构:

$x_{l+1} = LayerNorm(x_l + F(x_l))$

DeepNorm:

$x_{l+1} = \text{LN}(\alpha \cdot x_l + G_l(x_l, \theta_l))$

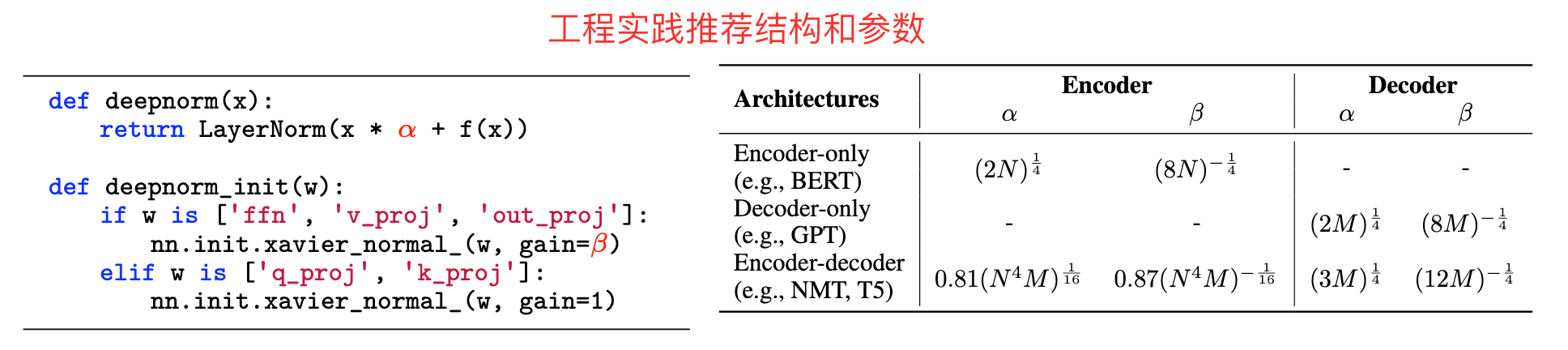
暂时不想细读这篇论文啦（后续补充）

思考：

DeepNorm中的 $\beta$ 是哪里的参数？

3.3 Group Norm

笔者理解：是对BN进行改进，将channel进行分组，然后组内Norm

论文链接：Group Norm

效果

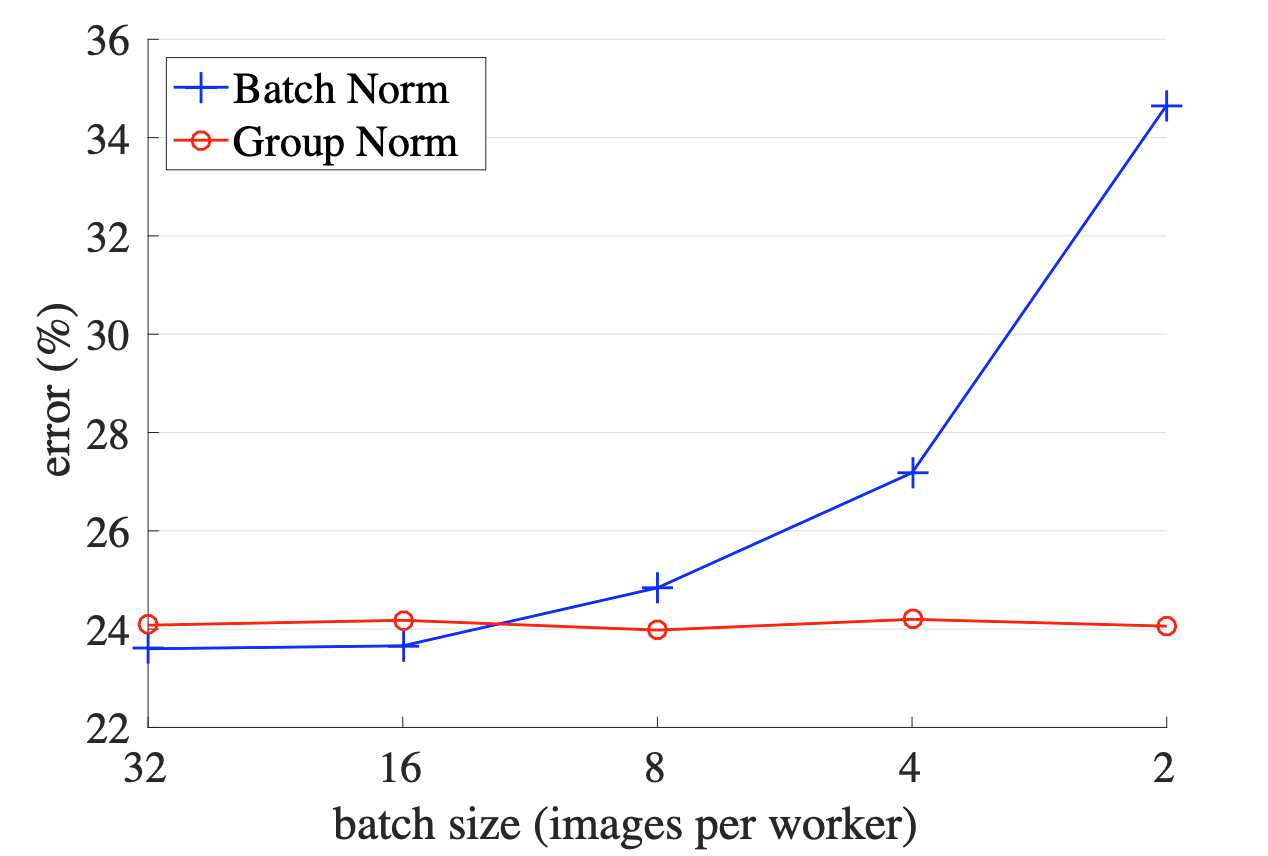
3.4 Instance Norm

没咋看，看论文是在CV领域用的

论文链接：Instance Norm

4. 代码实现

4.1 Batch Norm

python

class BatchNorm(nn.Module):
    def __init__(self, num_features, eps=1e-5, momentum=0.1):
        super(BatchNorm, self).__init__()
        self.num_features = num_features
        self.eps = eps

        self.gamma = nn.Parameter(torch.ones(num_features))  # 这俩是可学习参数
        self.beta = nn.Parameter(torch.zeros(num_features))
        self.momentum = momentum

        # 这里不使用buffer注册，用属性简单实现
        self.running_mean = torch.ones(num_features)
        self.running_var = torch.zeros(num_features)  

    def forward(self, x, training=True):
        if training:
            batch_mean = x.mean(dim=0)
            batch_var = x.var(dim=0, unbiased=False) # 计算时候无偏，存储时候有偏
            print("batch_mean shape, batch_var shape:", batch_mean.shape, batch_var.shape)
            self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * batch_mean
            self.running_var = (1 - self.momentum) * self.running_var + self.momentum * batch_var
            print("self.running_mean, self.running_var:", self.running_mean, self.running_var)

        else:
            batch_mean, batch_var = self.running_mean, self.running_var

        return self.gamma * (x - batch_mean) / (torch.sqrt(batch_var + self.eps)) + self.beta

  

if __name__ == '__main__':
    batch_norm = BatchNorm(10)
    ipt = torch.randn(size=(2, 10))
    print(ipt[1].shape)
    res = batch_norm(ipt)
    print(res)
    print(res.min(dim=0), res.max(dim=0))

4.2 Layer Norm

python

# 这里我只实现NLP的样式
class LayerNormImpl(nn.Module):
    def __init__(self, normalized_shape: tuple, eps=1e-5):
        super().__init__()
        self.eps = eps

        self.gamma = nn.Parameter(torch.ones(normalized_shape))
        self.beta = nn.Parameter(torch.zeros(normalized_shape))

    def forward(self, x):  # [batch_szie, seq_len, embedding_dim]
        emb_mean = x.mean(dim=-1, keepdim=True)
        emb_var = x.var(dim=-1, keepdim=True, unbiased=False)

        norm_x = (x - emb_mean) / (torch.sqrt(emb_var + self.eps))

        return self.gamma * norm_x + self.beta
        

if __name__ == '__main__':
    batch_size, seq_length, embedding_dim = 2, 5, 10
    embedding_size = [batch_size, seq_length, embedding_dim]
    ipt = torch.randn(batch_size, seq_length, embedding_dim)
    layer_norm = LayerNormImpl(embedding_size)
    out = layer_norm(ipt)
    print(out.shape)
    print(out.max(dim=-1), out.min(dim=-1))

4.3 RMS Norm

python

# 对Layer Norm的优化，采用均方根，并假设重新计算的中心化无关（去掉平移）
class RMSNorm(nn.Module):
    def __init__(self, normlized_shape: tuple, eps=1e-5):
        super().__init__()
        self.normlized_shape = normlized_shape
        self.eps = eps

        self.gamma = nn.Parameter(torch.ones(normlized_shape))

    def forward(self, x):
        # print(tuple(x.shape) == self.normlized_shape)
        assert tuple(x.shape) == self.normlized_shape, "归一化形状与输入形状不一致"

        rms = torch.sqrt(x.pow(2).mean(dim=-1, keepdim=True) + self.eps)
        
        return self.gamma *  x / rms
   

if __name__ == '__main__':
    batch_size, seq_length, embedding_dim = 2, 5, 10
    embedding_size = (batch_size, seq_length, embedding_dim)
    ipt = torch.randn(embedding_size)
    rms_norm = RMSNorm(embedding_size)
    out = rms_norm(ipt)
    print(out.shape)
    print(out.max(dim=-1), out.min(dim=-1))

NOTE

在工程中，RMSNorm会和输入之前的Linear操作放在一起执行，也就是分母直接换成上层的Linear操作

4.4 DyT

python

from torch.nn.functional import tanh

class DyT(nn.Module):
    def __init__(self, normlizated_shape: tuple, init_alpha=0.5):
        super().__init__()
        self.normlizated_shape = normlizated_shape
        self.alpha = nn.Parameter(torch.ones(1) * init_alpha)
        self.gamma = nn.Parameter(torch.ones(normlizated_shape))
        self.beta = nn.Parameter(torch.zeros(normlizated_shape))

    def forward(self, x):
        assert tuple(x.shape) == self.normlizated_shape, "输入形状与归一化形状不匹配"
        x = tanh(self.alpha * x)
        return self.gamma * x + self.beta 

    
if __name__ == '__main__':
    batch_size, seq_length, embedding_dim = 2, 5, 10
    embedding_size = (batch_size, seq_length, embedding_dim)
    ipt = torch.randn(embedding_size)
    dyt = DyT(embedding_size)
    res = dyt(ipt)

n. 面试问题

BN和LN有什么区别？

python

# PyTorch源码里面的说法值得借鉴一下
.. note::
    Unlike Batch Normalization and Instance Normalization, which applies
    scalar scale and bias for each entire channel/plane with the
    :attr:`affine` option, Layer Normalization applies per-element scale and
    bias with :attr:`elementwise_affine`.
    
# 当然，除了最后的`affine`的性质不同外，针对的归一化维度也不同
# 一个是在batch/channel维度，一个是在embedding维度(当然也可以在channel维度进行)，对应的应用场景不同

为啥不用BN来做NLP？
BN的训练和推理有什么不同？
讲讲Pre-Norm和Post-Norm。

model_framework

sum_knowledge

002_Normalization

1. 引入

1.1 为啥Norm？

1.2 作用

2. 类型

2.1 Batch Norm

2.2 Layer Norm

2.3 RMS Norm

2.4 DyT

3. 其他相关内容

3.1 Post-Norm & Pre-Norm

3.2 Deep Norm

3.3 Group Norm

3.4 Instance Norm

4. 代码实现

4.1 Batch Norm

4.2 Layer Norm

4.3 RMS Norm

4.4 DyT

n. 面试问题

002_Normalization

1. 引入 ​

1.1 为啥Norm？ ​

1.2 作用 ​

2. 类型 ​

2.1 Batch Norm ​

2.2 Layer Norm ​

2.3 RMS Norm ​

2.4 DyT ​

3. 其他相关内容 ​

3.1 Post-Norm & Pre-Norm ​

3.2 Deep Norm ​

3.3 Group Norm ​

3.4 Instance Norm ​

4. 代码实现 ​

4.1 Batch Norm ​

4.2 Layer Norm ​

4.3 RMS Norm ​

4.4 DyT ​

n. 面试问题 ​

1. 引入

1.1 为啥Norm？

1.2 作用

2. 类型

2.1 Batch Norm

2.2 Layer Norm

2.3 RMS Norm

2.4 DyT

3. 其他相关内容

3.1 Post-Norm & Pre-Norm

3.2 Deep Norm

3.3 Group Norm

3.4 Instance Norm

4. 代码实现

4.1 Batch Norm

4.2 Layer Norm

4.3 RMS Norm

4.4 DyT

n. 面试问题